Valine

ABSTRACT Spin inversion transfer (SIT) NMR experiments are reported probing the thermodynamics and kinetics of interconversion of two folded forms of a GCN4-like leucine zipper near room temperature. The peptide is ^sup 13^C^sup alpha^-labeled at position V9(a) and results are compared with prior findings for position L13(e). The SIT data are interpreted via a Bayesian analysis, yielding local values of T^sub 1a^, T^sub 1b^, k^sub ab^, k^sub ba^, and K^sub eq^ as functions of temperature for the transition Fa^sup V9^^sub a^F^sup V9^^sub b^ between locally folded dimeric forms. Equilibrium constants, determined from relative spin counts at spin equilibrium, agree well with the ratios k^sub ab^/k^sub ba^ from the dynamic SIT experiments. Thermodynamic and kinetic parameters are similar for V9(a) and Li 3(e), but not the same, confirming that the molecular conformational population is not two-state. The energetic parameters determined for both sites are examined, yielding conclusions that apply to both and are robust to uncertainties in the preexponential factor (kT/h) of the Eyring equation. These conclusions are 1) the activation free energy is substantial, requiring a sparsely populated transition state; 2) the transition state's enthalpy far exceeds that of either F^sub a^ or F^sub b^; 3) the transition state's entropy far exceeds that of F^sub a^, but is comparable to that of F^sub b^; 4) "Arrhenius kinetics" characterize the temperature dependence of both k^sub ab^ and k^sub ba^, indicating that the temperatures of slow interconversion are not below that of the glass transition. Any postulated free energy surface for these coiled coils must satisfy these constraints.

INTRODUCTION

Two-stranded coiled coils-comprising two parallel, registered ex-helices slightly supertwisted-are important models for addressing physical questions concerning protein folding (Lupas, 1996). The simplicity and linearity of the structure long since allowed the link between sequence and structure to be forged. The structure is based upon a pseudorepeating heptad of amino acids, designated abcdefg, in which residues a and d are hydrophobes and e and g oppositely charged (Crick, 1953; McLachlan and Stewart, 1975). The resulting pattern of hydrophobic and electrostatic interactions drives the dimerization.

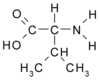
Among coiled coils, the GCN4 leucine zipper (called GCN4-1z here) has been especially thoroughly studied (O'Shea et al., 1989, 1991; Goodman and Kim, 1991; Kenar et al., 1995). In particular, we have employed a pseudowild-type version (called GCN4-1zK here) mutated at four sites: RIK, H18K, R25K, and R33K, and with 99% ^sup 13^C^sup alpha^ labels placed at selected sites as NMR targets (Lovett et al., 1996; Holtzer et al., 1997; d'Avignon et al., 1998). The full sequence of GCN4-1zK is given below.

The latter strategy has revealed several features of the population of conformational states as GCN4-1zK is heated, suggesting that it comprises more than two states: 1) at a given site, separate resonances appear for folded and unfolded species, allowing determination of site-specific thermal unfolding curves, curves that are seen to differ from site to site; 2) at most (but not all) sites, separate resonances appear for more than one folded form, allowing investigation of the thermodynamics and kinetics of interconversion of these folded substates.

Thus far, detailed study of the interconversion of two such dimeric folded substates has been reported for only one site: L13(e) (d'Avignon et al., 1998). That study was carried out by spin inversion transfer (SIT) NMR, resulting in determination of the equilibrium constant and rate constants (both ways) as functions of temperature for the process: F^sup L13^^sub 1^F^sup L13^^sub b^, wherein F^sup F13^^sub a^ signifies an ensemble of dimers folded at L13(e) in the form that dominates at moderate temperatures, and F^sup L13^^sub b^ signifies the corresponding ensemble folded at L13(e) in the form that dominates at moderate temperatures. Information in not yet available on the precise structural difference between these two dimeric folded forms.

If the interconversion of these two folded forms is a molecular-wide process, then corresponding data, taken at another site, would provide the same values for the rate and equilibrium constants and therefore the same activation parameters. Here, we test this idea by SIT studies at V9(a), a site distinct from L13(e), but in the same heptad. Specifically, we employ in this study the GCN4-1zK sequence: Ac-KLKQLEDKVEELLSKNYKLENEVAKLKKLVGEKAm, wherein each underlined residue-V9(a), L19(d), and G31(b)-bears a 99% ^sup 13^C^sup alpha^ label. Thus, we report here on the corresponding local process: F^sup V9^^sub a^F^sup V9^^sub b^.

If the interconversion of these two folded forms is a molecule-wide process, then corresponding data, taken at another site, would provide the same values for the rate and equilibrium constants and therefore the same activation parameters. Here, we test this idea by SIT studies at V9(a), a site distinct from L13(e), but in the same heptad. Specifically, we employ in this study the GCN4-1zK sequence: Ac-KMKQLEDKVEELLSKNYKLENEVAKLKKLVGEKAm, wherein each underlined residue-V9(a), L19(d), and G31(b)-bears a 99% ^sup 13^C^sup alpha^ label. Thus, we report here on the corresponding local process: F^sup V9^^sub a^F^sup V9^^sub b^.

As will be seen, the results indicate that the thermodynamic and kinetic parameters characterizing the transition between folded forms at V9(a) are similar to, but distinct from, those obtained for the related transition at L13(e). Once again, this suggests that a simple two-state picture is inadequate to describe the population of global molecular conformations in these coiled coils. Our data also allow certain conclusions to be drawn about the transition state ensemble for the interconversion, conclusions that apply to both sites.

MATERIALS AND METHODS

Synthesis, purification, and characterization of GCN4-1zK labeled at V9(a), L19(al), and G31(b)

Methods for solid-phase peptide synthesis, preparation of ^sup 13^C^sup alpha^-labeled Fmoc-amino acids, and purification and characterization of the completed, end-capped GCN4-1zK peptides have been described earlier (Holtzer et al., 1995, 1997; Lovett et al., 1996).

The molar mass of the purified peptide with 99% ^sup 13^C^sup alpha^ at positions V9(a), L19(d), and G31(b) was found to be 3947.6 Da (3947.5 Da, expected) by electrospray mass spectrometry. The purified peptide is >98% pure by reversed-phase high-performance liquid chromatography using a Vydac C18 column, as described earlier (d'Avignon et al., 1998). Its thermal CD unfolding profile is indistinguishable from that of the natural abundance and of other ^sup 13^C^sup alpha^-labeled GCN4-1zK peptides (Lovett et al., 1996). Solution concentrations, in formality of peptide chains, were determined from absorbance at 275 nm using an extinction coefficient of 1.40 cm^sup -1^ M^sup -1^.

^sup 13^C^sup alpha^-NMR

Bayesian data analysis

In the SIT experiment, the time course of restoration of the equilibrium is governed by four constants: the respective spin-lattice relaxation times at F^sup V9^^sub a^ and F^sup V9^^sub b^ (T^sup V9^^sub 1a^ and T^sup V9^^sub 1b^) and the rate constants for the forward (k^sup V9^^sub ab^) and reverse (k^sup V9^^sub ba^) conformational reactions F^sup V9^^sub a^F^sup V9^^sub b^. The modified Bloch differential equations appropriate to such a system and their solutions have long been known (McConnell, 1958; Rudin and Sauter, 1992). The form actually used here has been given earlier (d'Avignon et al., 1998).

The 32 FIDs for each temperature were subjected to joint Bayesian analysis, as characterized earlier (d'Avignon et al., 1998). This analysis produces the time course of longitudinal magnetization at each site (after inversion at each respective site) and the four rate constants. The method has already been described in detail (Bretthorst, 1990a-c, 1997).

RESULTS

Fig. 1 shows the relevant ^sup 13^C^sup alpha^-NMR spectra at the various temperatures employed. Our principal concern here is the region of resonances of residue V9(a). The complete range of resonances for this residue is marked from 62 to 69 ppm, as established earlier (Lovett et al., 1996; Holtzer et al., 1997). Near room temperature, resonances for two folded forms at V9(a) appear: F^sup V9^^sub a^ at 68 ppm, dominant at low temperature, and F^sup V(^^sub b^ at 67.5 ppm, dominant at moderate temperature. The resolution of resonances for the two folded forms at V9(a) is noticeably less than seen for the L13(e) site studied earlier (d'Avignon et al., 1998). It is noteworthy that the dominant form at low temperature is downfield from the other at V9(a), just opposite to the case of L13(e) studied earlier (d'Avignon et al., 1998). In this temperature range, the population of unfolded forms (near 63 ppm) is quite small.

In the particular peptide investigated here, residues L19(d) and G31(b) are also labeled. Their resonances appear in the range 54-59 and 44-47 ppm, respectively. The L19(d) resonance is unusual in that only one folded form is evident (Lovett et al., 1996; Holtzer et al., 1997). The G31(b) resonance region shows evidence of two poorly resolved folded forms (45.6-47 ppm), and of a small amount of unfolded form (45.5 ppm). Although we are principally concerned here with the V9(a) resonance, the others are a helpful check, since they must, and do, stay constant during the spin manipulations constituting the SIT experiments.

Fig. 5 shows the relevant values from Table 1 as a van't Hoff plot. The equilibrium constants for the F^sup V9^^sub a^F^sup V9^^sub b^ reaction from spin equilibrium data (open circles) agree well with those from the ratio of the rate constants (k^sub ab^/k^sub ba^, filled triangles). The fit of the combined data to the van't Hoff equation, assuming constant enthalpy, is also shown (solid line). The agreement between the equilibrium values and the kinetically determined ones is slightly less exact than in the case of the data for residue L13(e) done earlier (d'Avignon et al., 1998). We ascribe this to the somewhat poorer resolution of the two resonances seen in V9(a) and/or the somewhat lower concentration employed. The different, but similar, line for the L13(e) case is shown for comparison.

Fig. 6 displays Arrhenius plots of the rate constants k^sup V(^sub ab^ (open squares) and k^sup V9^^sub ba^ (filled diamonds), which are well fit by the Eyring equation (solid lines). Corresponding lines for the L13(e) site allow comparison. The relevant derived thermodynamic and kinetic parameters are shown in Table 2, along with previously determined values for site L13(e). It is apparent from Fig. 6 that the major difference between the two sites lies in the values of the forward rate constant, k^sub ab^.

DISCUSSION

Table 2 juxtaposes the thermodynamic and kinetic energetic parameters for position V9(a) with those obtained earlier for position L13(e). Fig. 7 summarizes this information pictorially. As can be seen, the general features of the transition are the same for both, but they differ in detail and the differences are outside the experimental errors. In particular, significant differences are seen in 1) the midpoint temperature for the transition ((Delta)T^sub m^ > 3 deg C); 2) the standard enthalpies and entropies of the overall transition (from the combined fits of the equilibrium and SIT experiments); 3) the activation entropies in the forward reaction direction; 4) the activation enthalpies and entropies in the reverse reaction direction.

The existence of more than two resonances at a given site (Lovett et al., 1996) and the observed differences in thermal unfolding curves at different sites (Holtzer et al., 1997) leave little doubt that the global equilibrium conformational ensemble in GCN4-1zK comprises more than two states. The present finding that the thermodynamic and kinetic energetic parameters for interconversion between folded states also depend on chain position underscores that conclusion.

The geometrical relationship between the two sites is schematically shown in Fig. 8, which represents a molecular cross-section at the level of the heptad containing V9(a) and L13(e). It may seem remarkable that two sites within the same heptad could display such differences. This finding implies a rather rich array of conformational states. Additional evidence for this conclusion already exists in the substantial local differences seen in amide proton exchange rates in parent GCN4-1z (Goodman and Kim, 1991). The latter study also concludes that dynamics can be markedly different from site to site.

Although results for the transitions at V9(a) and L13(e) are not in quantitative agreement, they are qualitatively similar. The values in Table 2 and Fig. 7 thus should allow certain conclusions to be drawn that apply to both. With regard to the thermodynamic parameters for the overall transition, it is clear that the standard enthalpy change for the transition is substantial, 15-20 kcal/mol, perhaps as much as one-third of the value for complete unfolding of the analogous molecule of GCN4-1z, as measured by calorimetry (Kenar et al., 1995). We do not as yet have comparable calorimetric data for GCN4-1zK. The overall entropy change is also large, its contribution exactly compensating the enthalpy near room temperature, specifically 27.2 deg C at V9(a) and 24.0 deg C at L13(e).

Turning to kinetic characteristics, one must recognize that some of the kinetic values in Table 2 depend not only on the kinetic data, but on the Eyring equation, which was used to interpret them. This equation gives for the rate constant in either direction

wherein kappa is the transmission coefficient, k Boltzmann's constant, h Planck's constant, and R the gas constant. The transmission coefficient measures the probability that the reaction will pass through the transition state in the product direction along the reaction coordinate and go on to products, as opposed to retracing its trajectory back through the transition state in the opposite direction. The value of this parameter is rarely known in kinetic investigations and is generally assumed to be near unity. We will do so here, and the issue will not be further discussed below.

It is axiomatic that the chemical kinetics of a particular reaction is dictated by the free energy surface of the system, a multidimensional surface rarely known, even in crude approximation, to the investigator. In absence of such knowledge, a general theory that mimics major features of the physics is desirable, and the Eyring theory has gained broad acceptance for the purpose. It has been widely used for over half a century to interpret data in all branches of chemistry.

For reactions involving conformational changes of macromolecules, the uncertainties are compounded by both the vast phase space involved and the small secondary-bond energies connecting neighboring states. There is certainly no kinetic theory of such reactions that has gained general acceptance. Simulations have been useful, but invariably employ drastically reduced representations of the molecular structure and of the free-energy surface. Consequently, some workers have used Eyring theory in this context (Tan et al., 1996; d'Avignon et al., 1998), but others have not (Chan and Dill, 1997; Oliveberg et al., 1998; Laurents and Baldwin, 1998). Indeed, it is fair to say that none of the terms normally encountered in a kinetic investigation-e.g., "transition state," "reaction coordinate"-has a clear meaning where protein folding is concerned. Different investigators use different definitions (Chan and Dill, 1998; Du et al., 1998; Laurents and Baldwin, 1998; Nymeyer et al., 1998).

Criticisms of Eyring theory have generally focused on the preexponential factor kT/h, whose numerical value near room temperature is ~6 X 10^sup 12^ s^supp -1^. Two grounds are usually presented for rejecting it. First, it is noted that the factor is often derived in the context of breaking an unstable covalent bond, and is therefore approximated as the inverse of the time for a single bond vibration, a derivation entirely inappropriate for protein folding transitions. Second, the Eyring theory is said to fail, because in the limit of zero Gibbs energy of activation, it requires the rate constant to be kT/h, i.e., of the order of 10^sup 12^ s^sup -1^, which is numerically far greater than for the fastest possible protein folding process. The latter is generally agreed to be the helix-coil transition, whose rate constant is ~10^sup 7^ s^sup -1^.

Although we certainly agree that no general theory of protein folding is yet available, we find this verdict on Eyring theory to be overly harsh. The preexponential in Eyring theory is essentially the reciprocal of the mean lifetime of the transition state. As such, approximating it as kT/h can be justified by other means than through bond vibrations (Weston and Schwarz, 1972). The uncertainty principle requires that (tau)(Delta)E>=h, wherein tau is the mean lifetime of the transition state and (Delta)E the uncertainty in its energy along the reaction coordinate. In Eyring theory, the transition state is considered to be in thermal equilibrium with the system, and therefore NE must be something like the root-mean-square variance of the energy distribution in one dimension, i.e., of the order of kT. Therefore, tau >= h/kT. Furthermore, Eyring theory postulates that the transition state is a maximum along the reaction coordinate, i.e., inherently unstable. Hence, the lower limit for the lifetime can be selected, giving as a crude approximation tau = h/kT, the same preexponential as before. Other derivations, more rigorous but less readily epitomized, yield the same result via arguments independent of bond vibrational considerations (Levine and Bernstein, 1987).

The second argument against Eyring theory is also questionable. The Eyring theory assumes that the transition state is an unstable state of free energy sufficiently large that it is sparsely populated, but a state that must be traversed (because it is the "least worst" way) to reach the reaction products. The entire theory rests on these assumptions and therefore on the proviso that (Delta)G(tt) >> RT. The Eyring equation therefore cannot be expected to reduce to the correct rate constant when the activation free energy is zero. The preexponential is of the order of the rate constant that would be observed, not if the activation free energy is zero, but if the entire molecular ensemble were to start in the transition state. This is not an experimentally accessible limit. It is therefore not correct to say that Eyring theory gives a rate constant of kT/h when (Delta)G(tt) = 0. The theory is, in fact, helpless in that regime. This limitation is perhaps more familiar in the case of bimolecular chemical reactions, where Eyring theory has also been quite successful, but certainly does not reduce to the Smoluchowski equation in the zero activation limit. It is easy to find cases wherein diffusion control leads to rate constants far below the 10^sup 12^ s^sup -1^ limit given in the Eyring equation. Yet, Eyring theory has been highly useful in such reactions when considerable activation is required. One must remember that the preexponential in a collision theory is independent of the free energy surface, whereas in Eyring theory it is the offspring of that surface.

It thus appears that, if the transition state ensemble for protein conformational changes can be viewed as an unstable state of high free energy, then use of the Eyring equation may be justified. However, it is certainly not clear that even these minimalist requirements are met for protein folding. Consequently, it is necessary to inquire as to the effects of failure of the Eyring equation on our conclusions.

It should first be noted that the existence of T in the Eyring preexponential is essentially immaterial. The temperature dependence introduced by this linear term is negligible compared to the exponential dependence in the enthalpy term. Second, it is evident from the form of the Eyring expression that a change in the preexponential affects the values (as obtained from fitting data) of (Delta)G(tt) and *delta)S(tt), but not (Delta)H(tt). In order to estimate the effect of failure of the Eyring equation, we therefore recalculated these values, changing the preexponential to 10^sup 7^ s^sup -1^, mimicking the fastest process involved in folding. Since this new value is actually a measured rate constant, it includes both exponential and preexponential factors. It therefore represents a lower limit to the proper preexponential, just as kT/h represents an upper limit.

The results of the recalculation are very similar for both sites, V9(a) and L13(e), so they can be discussed together. The value of AG: changes appreciably from 17 to 9.3 kcal/mol, but is still substantial. The entropy ascribed to the transition state is no longer 20% less, but rather 25% more, than that of Fb. However, the enthalpy of the transition state remains 70-90% higher than for Hb.

The following conclusions concerning the kinetics are therefore robust, surviving possible deficiencies in the Eyring equation.

These data thus allow a beginning to be made toward determination of some of the characteristics of the free energy surface of these two-stranded coiled coils, in particular the activation parameters for the transition between two folded forms at two different sites. Many current studies have similar aims for these and other proteins. It is perhaps worth mentioning that the methods employed here do not rely on assumptions concerning the effects of denaturants or of mutations on the kinetics, as do approaches confined to data at a single temperature. We feel strongly that conclusions are more certain when temperature is employed as an experimental variable, since then the activation enthalpy, at the very least, can be determined with a high degree of certainty. It is legitimate to inquire about the generality of our findings. Might globular proteins also exhibit such local differences in overall unfolded fraction and even distinct, local, interconverting folded forms? At present, we cannot say for sure, but our surmise is that such conformational complexity will be found in some globular proteins as well, but will be more commonly seen in proteins with relatively simple topologies such as the two-stranded coiled coils. One must remember that the conclusion that a conformational population is two-state rests on the choice of a baseline for some physical property, a choice often made so as to exclude all but the most highly cooperative change. In that sense, the conclusion is as much a product of that choice as of the system itself.

Finally, it may be worth noting that the type of local interconversion of folded forms seen here occurs in the near-physiological range. It is possible, therefore, that the dynamics we observe are as significant for protein function as for folding per se.

Mass spectrometry was provided by the Washington University Mass Spectrometry Resource, a National Institutes of Health Research Resource (Grant P41RR0954). Synthesis of the peptide was carried out by Dr. Eva Lovett. Development of the Bayesian techniques employed here was supported by National Institutes of Health Grant NS-35912 and by a license agreement with Varian Associates. One of us (A.H.) acknowledges informative discussions on Eyring theory with Prof. Robert Yaris and the continuing aid of the Luftmensch Society.

REFERENCES

Bretthorst, G. L.1990a. Bayesian analysis. I. Parameter estimation using quadrature NMR models. J. Magn. Reson. 88:533-551. Bretthorst, G. L.1990b. Bayesian analysis. II. Model selection. J. Magn.

Reson. 88:552-570.

Bretthorst, G. L.1990c. Bayesian analysis. III. Applications to NMR signal detection, model selection, and parameter estimation. J. Magn. Reson. 88:571-595.

Bretthorst, G. L. 1997. Bayesian analysis software package user guide. Pub. No. 87-190172-00. Rev. A0197, Varian Associates, Palo Alto, CA. Chan H. S., and K. A. Dill. 1997. From Levinthal to pathways to funnels.

Nat. Struct. Biol. 4:10-19.

Chan, H. S., and K. A. Dill. 1998. Protein folding in the landscape perspective: chevron plots and non-Arrhenius kinetics. Proteins. 30:2-33. Crick, F. 1953. The Fourier transform of a coiled coil. Acta Crystallogr. 6:689-697.

d'Avignon, D. A., G. L. Bretthorst, M. E. Holtzer, and A. Holtzer. 1998. Site-specific thermodynamics and kinetics of a coiled-coil transition by spin inversion transfer NMR. Biophys. J. 74:3190-3197. Du, R., V. S. Pande, A. Y. Grosberg, T. Tanaka, and E. S. Shakhnovich. 1998. On the transition coordinate for protein folding. J. Chem. Phys. 108:334-350.

Goodman, E. M., and P. S. Kim. 1991. Periodicity of amide proton exchange rates in a coiled-coil leucine zipper peptide. Biochemistry. 30:11615-11620.

Holtzer, M. E., D. L. Crimmins, and A. Holtzer. 1995. Structural stability of short subsequences of the tropomyosin chain. Biopolymers. 35: 125-136.

Holtzer, M. E., E. G. Lovett, D. A. d'Avignon, and A. Holtzer. 1997. Thermal unfolding in a GCN4-like leucine zipper: '3Ca-NMR chemical shifts and local unfolding equilibria. Biophys. J. 73:1031-1041.

Kenar, K. T., B. Garcia-Moreno, and E. Freire. 1995. A calorimetric characterization of the salt dependence of the stability of the GCN4 leucine zipper. Protein Sci. 4:1934-1938.

Laurents, D. V., and R. L. Baldwin. 1998. Protein folding: matching theory and experiment. Biophys. J. 75:428-434.

Levine, R. D., and R. B. Bernstein. 1987. Molecular Reaction Dynamics

and Chemical Reactivity. Oxford University Press, New York. 173-190. Lovett, E. G., D. A. d'Avignon, M. E. Holtzer, E. H. Braswell, D. Zhu, and A. Holtzer. 1996. Observation via one-dimensional '3C'-NMR of local conformational substates in thermal unfolding equilibria of a synthetic analog of the GCN4 leucine zipper. Proc. Natl. Acad. Sci. USA. 93: 1781-1785.

Lupas, A. 1996. Coiled coils: new structures and new functions. TIBS. 21:375-382.

McConnell, H. M. 1958. Reaction rates by nuclear magnetic resonance. J. Chem. Phys. 28:430-431.

McLachlan, A. D., and M. Stewart. 1975. Tropomyosin coiled-coil interactions. Evidence for an unstaggered structure. J. Mol. Biol. 98:293-304. Nymeyer, N., A. E. Garcia, and J. N. Onuchic. 1998. Folding funnels and frustration in off-lattice minimalist protein landscapes. Proc. Natl. Acad. Sci. USA. 95:5921-5928.

Oliveberg, M., Y-J. Tan, M. Silow, and A. R. Fersht. 1998. The changing nature of the protein transition state: implications for the shape of the free-energy profile for folding. J. Mol. Biol. 277:933-943. O'Shea, E. K., J. D. Klemm, P. S. Kim, and T. Alber. 1991. X-ray structure of the GCN4 leucine zipper, a two-stranded, parallel coiled coil. Science. 254:539-544.

O'Shea, E. K., R. Rutkowski, and P. S. Kim. 1989. Evidence that the leucine zipper is a coiled coil. Science. 243:538-542. Rudin, M., and A. Sauter. 1992. Measurement of reaction rates in vivo using magnetization transfer techniques. In NMR Basic Principles and Progress. P. Diehl, E. Fluck, H. Ginther, R. Kosfeld, and J. Seelig editors. 27:257-293.

Tan, Y-J., M. Oliveberg, and A. R. Fersht. 1996. Titration properties and thermodynamics of the transition state for folding: comparison of twostate and multi-state folding pathways. J. MoL BioL 264:377-389. Weston, R. E., and H. A. Schwarz. 1972. Chemical Kinetics. Prentice-Hall, Englewood Cliffs, NJ.

D. Andre d'Avignon, G. Larry Bretthorst, Marilyn Emerson Holtzer, and Alfred Holtzer Department of Chemistry, Washington University, St. Louis, Missouri 63130 USA

Received for publication 2 October 1998 and in final form 29 January 1999.

Address reprint requests to Alfred Holtzer, Department of Chemistry, Washington University Campus Box 1134, One Brookings Drive, St. Louis, MO 63130-4899. Tel.: 314-935-6572; Fax: 314-935-4481; E-mail: holtzer@wuchem.wustl.edu.

Copyright Biophysical Society May 1999
Provided by ProQuest Information and Learning Company. All rights Reserved